חידות בינוניות

היהפכו שלושה לשישה?

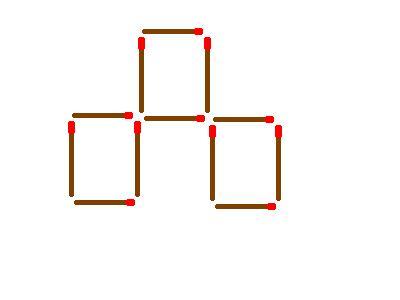
_12__copy_copyלפניכם שלושה ריבועים המורכבים מ-12 גפרורים:

כיצד אפשר להכפיל את מספר הריבועים מבלי להוסיף גפרורים?

במילים אחרות, עליכם להרכיב מ-12 הגפרורים שישה ריבועים

מבלי לשבור את הגפרורים, מבלי לשים גפרור על גפרור

ומבלי להשאיר  "זנבות" של גפרורים?

 

+ - רמז דק Click to collapse

תחשבו על מבנה גאומטרי שרואים בו שישה ריבועים...

+ - רמז עבה Click to collapse

תחשבו בתלת מימד...

+ - פתרון Click to collapse

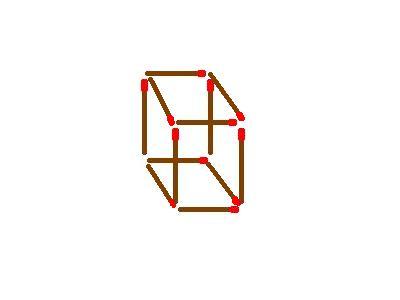_12__אפשר להרכיב מבנה תלת מימדי- קובייה.

לקובייה שש פאות וכל פאה בצורת ריבוע....

הוספת תגובה

תגובות (5)

  • שני

    הדרישה היתה לא לשים גפרור על גפרור, בפתרון הקוביה יש שני גפרורים העולים וחוצים גפרורים אחרים. נכון רק תאורטית, לא מעשית!

    0
    השב
    דיווח
    כתובת URL מקוצרת:

  • הרפתן

    בונים קוביה

    1
    השב
    דיווח
    כתובת URL מקוצרת:

  • לאמשנה....

    לוקחים את שלושת הגפרורים מהריבוע שלמעלה ושמים שניים בתוך ריבוע אחד מהריבועים שלמטה כך שיוצא 4 ריבועים בתוך הריבוע ואת הגפרור השלישי שמים למטה בין שני הריבועים שלמטה וכך יש 2 ריבועים רגילים ועוד אחד מחולק ל 4 4+2=6!!!!!!

    1
    השב
    דיווח
    כתובת URL מקוצרת:

  • סלוודור

    א"א לקרוא למלבן ריבוע

    1
    השב
    דיווח
    כתובת URL מקוצרת:

  • מושון

    אם מניחים שהריבועים אינם שוים (אין דרישה כזו) . אז ניתן לבנות

    ריבוע שאורך כל צלע בו באורך 2 גפרורים ואז 4 ריבועים פנימיים
    _ _
    | _|_| ונקודת המפגש בין הגפרורים במרכז יוצרת ריבוע 6
    | _|_|

    1
    השב
    דיווח
    כתובת URL מקוצרת:

חדשות ועדכונים

טיפים לבחירת מזגן חדש
טיפים לבחירת מזגן חדש
המזגן הוא אינו עוד מוצר חשמלי, אלא חלק משמעותי בתשתית הבית, ויש להתייחס אליו בהתאם בעת רכישת מזגן חדש. להלן מספר טיפים ומידע...
האם כדאי לקחת ייעוץ משכנתאות?
האם כדאי לקחת ייעוץ משכנתאות?
כשמחשבים את כל הוצאותיכם על משכנתאות כדאי לקחת בחשבון גם ייעוץ משכנתא
תהליך אישור תוספת בנייה על הגג
תהליך אישור תוספת בנייה על הגג
לא מעט ישראלים מנצלים את העובדה שהם מתגוררים בקומה עליונה, על מנת ליהנות מתוספת בנייה על הגג. הרעיון הוא מאוד פשוט. במבנים רבים,...
קייטרינג עם מלצרים – כיצד לבחור את החברה הנכונה
קייטרינג עם מלצרים – כיצד לבחור את החברה הנכונה
כשאנחנו עורכים אירוע פרטי, עסקי או כל אירוע אחר, אחד הספקים, נותני השירותים איתה נצטרך לעבוד זו חברת קייטרינג.
ילדיכם במערכות החינוך השונות אך לא מצליחים להתאקלם כמו כולם?
ילדיכם במערכות החינוך השונות אך לא מצליחים להתאקלם כמו כולם?
שנת הלימודים החדשה התחילה והילדים שלכם מתחילים מסגרות. ישנם ילדים אשר נשארים במסגרות חינוכיות שכבר למדו בהן בשנים הקודמות וישנם ילדים אשר מתחילים...
טיול רומנטי על סגווי בירושלים
טיול רומנטי על סגווי בירושלים
ירושלים, בירת ישראל, היא בין הערים האטרקטיביות ביותר בעולם, ומה יותר מיוחד מטיול רומנטי על סגווי בירושלים?