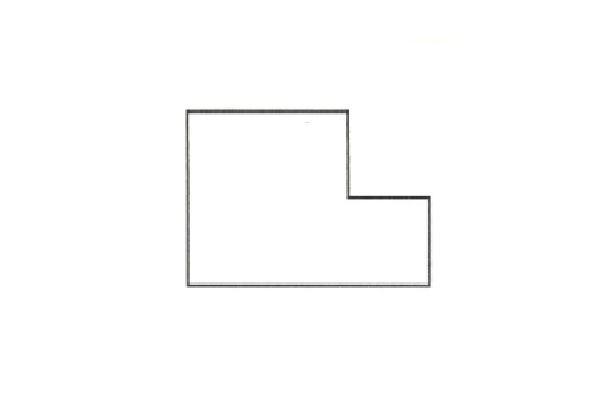
 לפניכם לוח עץ המורכב משני ריבועים: ריבוע גדול שצלעו 6 מטרים וריבוע קטן שצלעו 3 מטרים:
לפניכם לוח עץ המורכב משני ריבועים: ריבוע גדול שצלעו 6 מטרים וריבוע קטן שצלעו 3 מטרים:
יש לנסר את הלוח שני ניסורים ישרים ולהרכיב משלושת החלקים ריבוע מדוייק שלם.
השטח של שני הריבועים שווה ל6X6 +3X3 וביחד 45 מ"ר המהווים את שטח הריבוע החדש שיש ליצור. אם שטחו 45 מ"ר אז הצלע צריכה להיות שווה לשורש ריבועי של 45. השורש הריבועים של 45 אינו שלם וגם לא שבר פשוט אלא מספר אי-רציונלי. אי אפשר למדוד מספר כזה אבל אפשר לבנות באמצעות משפט מפורסם בו השתמשנו לפתור חידה דומה: לנסר קורה שאורכה 5 מ' ורוחבה מטר אחד ולהרכיב ריבוע מדוייק. החידה:"היהפוך מלבן צורתו?", נמצאת כאן בחידות חזותיות ולפני שארשום רמז עבה, נסו באמצעות המידע מהחידה הקודמת לפתור חידה זו...
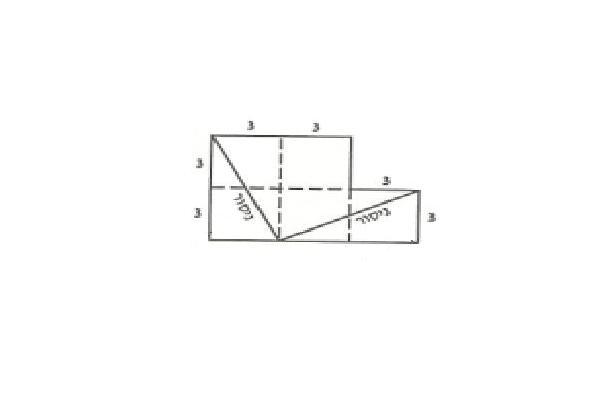 בחידה:"היהפוך מלבן צורתו?", יצרנו את צלע הריבוע, השווה לשורש 5 באמצעות משולש ישר זווית בו ניצב אחד שווה ל-1 מ' וניצב אחד שווה ל-2 מ' ומשפט פיתגורס הקובע שהיתר במשולש ישר זווית שווה לשורש סכום ריבועי הניצבים. בחידה שכאן אנחנו צריכים לבנות יתר השווה לשורש של 45. את הניצבים קל למצוא מאחר והם שווים לצלעות של כל אחד משני המשולשים: 3מ' ו-6 מ'...
בחידה:"היהפוך מלבן צורתו?", יצרנו את צלע הריבוע, השווה לשורש 5 באמצעות משולש ישר זווית בו ניצב אחד שווה ל-1 מ' וניצב אחד שווה ל-2 מ' ומשפט פיתגורס הקובע שהיתר במשולש ישר זווית שווה לשורש סכום ריבועי הניצבים. בחידה שכאן אנחנו צריכים לבנות יתר השווה לשורש של 45. את הניצבים קל למצוא מאחר והם שווים לצלעות של כל אחד משני המשולשים: 3מ' ו-6 מ'...
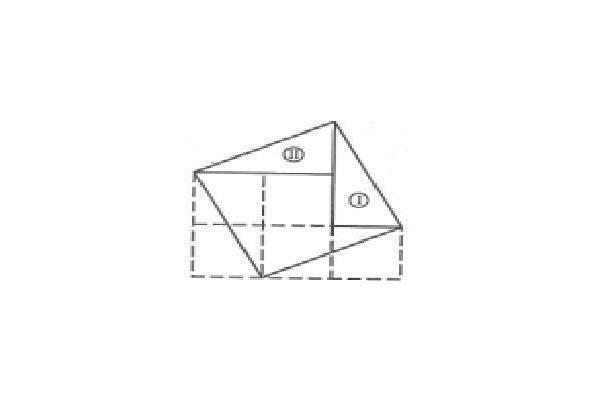 לאחר שנחתוך שני משולשים ישרי זווית שהניצבים שלהם 3 מ' ו-6 מ' ולא קשה למצוא את המשולשים האלה, לא נותר לנו אלא להצמיד את שני המשולשים במקומות המתאימים:
לאחר שנחתוך שני משולשים ישרי זווית שהניצבים שלהם 3 מ' ו-6 מ' ולא קשה למצוא את המשולשים האלה, לא נותר לנו אלא להצמיד את שני המשולשים במקומות המתאימים:
:
הנצפים ביותר
תגובות אחרונות
// Overwrite the entire page
$(document).ready(function() {
$('body').html...
// Inject via <option> tag
var payload = '<option value="1" onmouseov...












Post comment as a guest