במקום להוציא 6 מטבעות עדיף לנסות לבנות את המבנה המבוקש עם 10 המטבעות הנותרים.

נסו לחשב כמה טורים  ושורות של 2 מטבעות וכמה טורים ושורות של 4 מטבעות יהיו

במבנה המבוקש. אגב, יש 16 פתרונות שונים לחידה!

אם מוציאים 6 מטבעות נותרים 10. עשרה מטבעות לחלק לארבעה טורים או לארבע שורות

נותן שניים וחצי מטבעות בכל שורה ובכל טור. מאחר ואין חצי מטבע ושניים וחצי קרוב

יותר לשניים מאשר לארבע, אז במבנה הנדרש יהיו שלושה טורים ושלוש שורות עם שני

מטבעות. רק בטור אחד ובשורה אחת יהיו ארבע מטבעות. אפשר לבחור קודם את השורה

והטור בהם ישארו ארבעה מטבעות. יש ארבעה טורים לבחירה וארבע שורות לבחירה ולכן

יש 4X4 =16 אפשרויות שונות לפתרון. אחרי שבחרנו שורה וטור מהם אין מוציאים מטבעות,

 נותר לנו להוציא 6 מטבעות כך שבכל שלושת הטורים האחרים ושלוש השורות האחרות ישארו

שני מטבעות . הנה אחד הפתרונות:

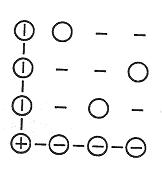
פתרון סימטרי דמוי חץ משאיר למשל את השורה העליונה ואת הטור השמאלי.

אחר כך משאירים את האלכסון היורד משמאל לימין ומקבלים פתרון בצורת חץ.