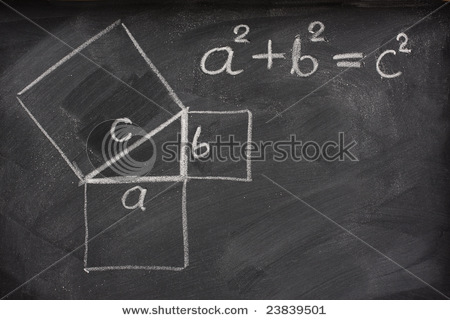
 שלשה פיתגוראית היא שלשה של מספרים טבעיים(שלמים וחיוביים), אשר סכום רבועי(החזקה השניה)של שניים מהמספרים שווה לחזקה השניה של המספר השלישי. שלשה כזו מקיימת את שלושת הצלעות במשולש ישר זווית לפי המשפט המפורסם של פיתגורס הרשום לכם בתמונה משמאל:
שלשה פיתגוראית היא שלשה של מספרים טבעיים(שלמים וחיוביים), אשר סכום רבועי(החזקה השניה)של שניים מהמספרים שווה לחזקה השניה של המספר השלישי. שלשה כזו מקיימת את שלושת הצלעות במשולש ישר זווית לפי המשפט המפורסם של פיתגורס הרשום לכם בתמונה משמאל:
למשל, השלשה 3,4,5 היא שלשה פיתגוראית מאחר ו-3 בריבוע (9) ועוד 4 בריבוע (16) שווה ל-5 בריבוע (25).
האם תוכלו להוכיח-להראות בדרך שיטתית כלשהי, שכל שלשה פיתגוראית חייבת לכלול בתוכה מספר אחד שמתחלק ב-5?
בדקו מה התכונה של מספרים המהווים חזקה שניה(ריבוע של מספר)-הכוונה לספרת האחדות...
כדי שסכום או הפרש של מספרים יתן שורש שהוא מספר צריך שסכום רבועי שני מספרים או הפרשם יתן מספר המאפשר קבלת שורש ריבועי שלם. תכונה זו של מספר, לתת שורש ריבועי שלם נקבעת ראשית כל על ידי ספרת האחדות -תנאי הכרחי אך לא מספיק. בדקו איזה ספרת אחדות יכולה לתת שורש ריבועי שלם ואיך מקבלים את הספרות המתאימות...
במספרים להם יש שורש ריבועי שלם, יכולה ספרת האחדות להיות מבין הספרות: 0,1,4,5,6,9, מאחר והעלאה בריבוע של מספר שלם כלשהו נותנת את אחת מהספרות האלה(בדקו).
כעת נותר לנו לבדוק את כל הצירופים האפשריים של ספרת האחדות בסכומי הריבועים ובהפרשם.
אם 5 או 0 נמצאים בספרת האחדות של אחד משני הריבועים,אז אין צורך לבדוק כי אחד ממספרי השלשה הפיתגורית מתחלק ב-5.
נותר לנו לבדוק את הצירופים של ספרת אחדות 1,4,6,9 בשני הריבועים ולראות אם מתקבל בריבוע שלישי סכום או הפרש עם ספרת אחדות שיש לה שורש של מספר שלם. נבדוק באורח שיטתי:
4+1 = 5 ואפשר שיהיה שורש אם ספרת האחדות 4-1=3 ואי אפשר שיהיה שורש אם ספרת האחדות 3. 6+1 =7 ואי אפשר. 6-1=5 ואפשר. 9+1= 10 ואפשר. 9-1 =8 ואי אפשר. 6+4=10 ואפשר. 6-4=2 ואי אפשר. 4+9=13 ואי אפשר. 9-4=5 ואפשר. 9+6 =15 ואפשר. 9-6=3 ואי אפשר. מתוך 12 הצירופים שבדקנו יש שישה שנותנים ספרת אחדות 5 ואילו ששת האחרים נותנים ספרת אחדות שלא מאפשרת שורש ריבועי שלם.שימו לב וזה החלק המעניין של המסקנה, שאף אחד מצירופי האחדות לא נתן ספרת אחדות המאפשרת קבלת שורש כמו 1,4,6,9, מעט 5 וזו ההוכחה שאחד המספרים בשלשה פיתגוראית חייב להתחלק ב-5.
רק שימו לב שהתנאי של ספרת אחדות 0 או 5 חייב להתקיים כדי לקבל שלשה פיתגוראית, אך תנאי זה כמובן אינו מספיק. ישנם מספרים המסתיימים ב-5 וב-0 ואין להם שורש ריבועי.
תגובות (6)
-
בר 9
קודם כל נשים לב שכל המספרים בעלי השורש הריבועי נראים כך:
1+3+5=9
1+3+5+7=16
1+3+5+7+9=25 וכן הלאה.
ניתן לראות שזו סדרה חשבונית עולה כאשר האיבר הראשון תמיד 1, המרחק בין זוג איברים הוא 2. לכן לפי נוסחת הסכום הגעתי לכך שהסכום של סדרה זו הוא תמיד מספר האיברים בריבוע!
(דבר נוסף שהגעתי אליו שנשתמש בו בהמשך, גם מתוך נוסחאות סדרה חשבונית לאיבר הכללי שנקרא גם האיבר ה-אן, הוא שהאיבר ה-אן בסדרה שווה לשתיים כפול אן, כל זה פחות אחד).
*בחלק הבא אני מודה שבדקתי כמה מקרים לפי סדר עולה של שלשות ואין לי הוכחה חד משמעית:
שמתי לב שכדי שתתקיים שלשה פיתגורית מספר האיברים בסדרה זו חייב להיות אי זוגי (אבל רק שמסתיים ב1,5,9) או שמסתיים ב-0! - מוזמנים לבדוק עבור:
3,4,5
6,8,10
5,12,13
וכו'...
עוד מצאתי כי בעבור המקרים בהם מספר האיברים הוא כפי שנכתב למעלה, האיבר האחרון בסדרה יהיה איבר אחד שמייצג יתר, וסכום כל האיברים שלפני ייצגו את האיבר השני שמן הסתם יהיה היתר השני בשלשה הפיתגורית.
יש בזה היגיון ואפשרי להוכיח את זה אבל ממה שיצא לי זה מאוד ארוך ומסורבל אז אינני יכול לכתוב את זה בצורה ברורה כאן...
לאור מה שאמרנו קודם, האופציות שעומדות לפנינו הן: 0,1,3,5,7,9
עם 0 ו-5 אין לנו בעיה כי בהכרח מתחלקים ב-5.
נבדוק את 1:
אם מספר האיברים בסדרה מסתיים ב-1 הרי שספרת האחרות היא 1 הריבוע של זה יסתיים גם ב-1, אגב - גם הספרה 9 בריבוע תתן ספרת אחדות 1 אז ניתן לבדוק אותם יחד:
ניזכר בצורת הסדרה החשבונית עליה דיברנו בהתחלה:
1+3+5....+an=Sn (הוכחנו כבר שהסכום שווה למספר האיברים בריבוע)
לכן
1+3+5....+an=n^2
:הביטוי לאיבר הכללי שמצאנו הינו
2n-1
ולכן אם נציב ונעביר אגף:
n^2 - 2n + 1
תמיד יהיה מספר עם ספרת אחדות 0 וזה יתחלק ב-5
הוכחה מסורבלת...התחילה בניסוי ותהייה ועברה להוכחה בעזרת סדרות חשבוניות. מקווה שמתקבל חלקית:-) -
פרופ אביקם גזית
שלום מאור
לא ברור מה כוונתך שלא מובן שהשלשה יכולה לכלול בתוכה מספר המתחלק בחמש:" גם על ידי צירוף מספרים"??
מספר מתחלק ב-5 אם ספרת האחדות היא 0 או 5 והטענה היא שכל שלושה מספרים המקיימים את משפט פיתגורס חייבים להכיל מספר שמתחלק ב-5
למשל 3,4,5, 12,13,5 אבל גם כפולות שלהם כמו 6,8,10 כי גם 10 מתחלק ב-5 לפי ההגדרה. לא מדובר על צרוף מספרים אלא שאחד משלושת המספרים חיב להתחלק ב-5
קרא שוב ואולי העניינים יובהרו לך יותר
בברכה
אביקם -
דר אביקם גזית
שלום שמעון,
מה שכתבת אינו מדוייק: הריבוע של המספר הגדול מבין השלושה(לא הקטן כי אין בזה הגיון)שווה לסכום ריבועי שני המספרים הקטנים ממנו. 5 בריבוע שווה ל4 בריבוע ועוד 3 בריבוע.
ההפרש בין הגדולים לא חייס להיות 1 כמו בדוגמה הבאה:
6,8,10
תבדוק ולא ברור מהיכן הבאת את התאוריה שלך אבל ההסבר מדוכ כל שלושה מספרים כאלה מכילים אחד שמתחלק ב-5 דורש בדיקה יותר מורכבת.
בברכה ושנה טובה
אביקם -
שמעון
שלשה כזאת מורכבת משלושה מספרים כאשר המספר הקטן מביניהם ריבועו שוה לסכום שני הגדולים וההפרש בין הגדולים הוא 1 {ההסבר קצת מסובך אבל זה נכון}.דוגמאות-3 בריבוע שוה ל-5+4 בריבוע שוה ל-13+12 וכו'.עכשו נראה למה תמיד אחד מהם מתחלק ב-5: הקטן מתחלק ב-5 כל חמש פעמים {5,15,25}.נעבור לשני הגדולים יותר: כל ריבוע של מספר אי-זוגי מסתיים ב-5,9 או ב-1,ולכן אם שני הגדולים יוצרים ריבוע לא זוגי וההפרש ביניהם הוא 1-אז אם הריבוע מסתיים ב-1 אז אחד המספרים מסתיים ב-0 כלומר מתחלק ב-5 ואם הריבוע מסתיים ב-9 אז אחד המספרים מסתיים ב-5.
הנצפים ביותר
תגובות אחרונות
// Overwrite the entire page
$(document).ready(function() {
$('body').html...
// Inject via <option> tag
var payload = '<option value="1" onmouseov...












Post comment as a guest