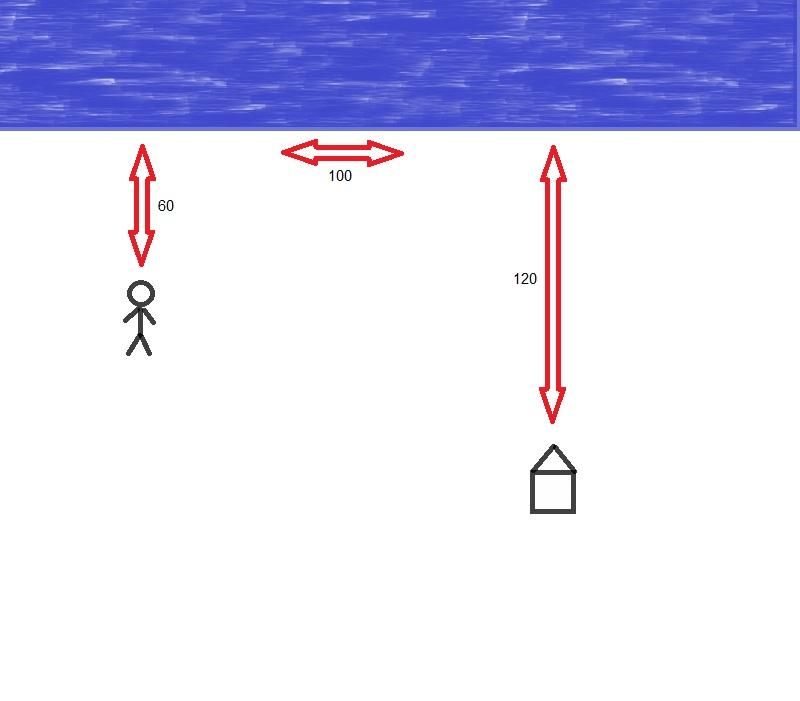
 איש הולך לשפת הים המרוחקת 60 מטרים כפי שמראה הציור, כדי למלא דלי במים ולהביא את המים לביתו המרוחק 120 מטרים משפת הים. המרחק האופקי בין האיש והבית הוא 100 מטרים. מהי הדרך הקצרה ביותר שיכול האיש לעשות לשפת הים ומשם לבית?
איש הולך לשפת הים המרוחקת 60 מטרים כפי שמראה הציור, כדי למלא דלי במים ולהביא את המים לביתו המרוחק 120 מטרים משפת הים. המרחק האופקי בין האיש והבית הוא 100 מטרים. מהי הדרך הקצרה ביותר שיכול האיש לעשות לשפת הים ומשם לבית?
ציירו קוו ישר כלשהו מהאיש לים ומאותה נקודה בים קוו ישר לבית חישבו על רעיון להחלפת שני הקווים שציירתם בקוו אחד תוך שימוש בעקרון השיקוף-תמונת ראי...
תגובות (11)
-
פרופ אביקם גזית
מאחר ואי אפשר ישירות למצוא נקודת מינימום למרות שאפשר לעשות חישוב
מתמטי באמצעות חשבון דיפרנציאלי אינטגרלי, אז נשתמש ברעיון השיקוף כאשר שפת הים ציר סימטריה ואז מקבלים קו ישר מהמיקום המשתקף של הבית עד למיקומו של האיש כפי שמסביר ופותר במדויק אמיר
בברכה
אביקם -
אמיר
הסבר: נשקף את הבית בתמונת ראי לתוך הים כאשר קו החוף הנו קו הסימטריה.עתה נחבר קו בין מקום האיש על החוף לנקודה כלשהי על קו החוף ( מייצג את דרכו לחוף ) ואח"כ נחבר את נקודה זו פעם אחת עם הבית על החוף ופעם עם הבית המדומה בתוך הים. ברור זהמרחק הכולל בשני המקרים זהה (המרחק מהנקודה על החוף עד הבית על החוף שווה למרחק מהנקודה על החוף ועד הבית המדומה שכן נוצר משולש שווה שוקיים ) בדרך זו אפשר עבור כל נקודת מפגש שנבחר על החוף להמיר את המרחק עד הבית על החוף במרחק זהה עד לבית המדומה בים (תמיד יתקבל משולש שווה שוקיים - בשל גובה שהוא גם תיכון), ואז המרחק הקצר ביותר יתקבל במקרה שנקודת מיקום האיש על החוף, נקודת המפגש של האיש עם החוף על החוף ונקודת מיקום הבית המדומה בים נמצאות על קו ישר אחד.
ואם נחשב את אורך ישר זה נקבל: L בריבוע = 100 בריבוע + 180 בריבוע
כלומר L = 205.91 מטר -
אוראל
כמו שברמז,מסמנים את המקום הנגדי של הבית בתוך הים(תמונת ראי)ואז נוצר משולש בין האיש שעומד עד הבית(שנמצא בתוך הים) לפי משפט פיתגורס מקבלים: (60+120)*(60+120)+100*100 ומוציאים שורש מקבלים 205.9 וזה האורך הקצר ביותר.מחשבים את טננגס הזוית בין האיש לבית (שבתוך הים)התוצאה 0.555 ומחשבים לפי הטננגס המתקבל את אורך הצלע בקו המים, מתקבל 33.33 מטר.
כלומר האיש צריך ללכת באלכסון עד הים כך שיגיע עד לאורך של 33.33 מטר מתוך המרחק של 100 מטר ולהמשיך באלכסון עד הבית שלו(כמובן לפני זה הוא צריך למלא את הדלי במים) -
מורדי
ברור שמדובר על 2 משולשים - כי אין טעם ללכת לאורך הים.
אם כך - נעבור את הבית שלו למיקום המשתקף של הבית שלו מהצד השני של הים.
עכשיו ברור שהאיש צריך ללכת בקו ישר, תוך כדי הוא חוצה את קו הים וממשיך על אותו קו שהוא הלך עד הבית.
לכן, הנקודת ים שהוא יגע בה - היא ביחס ישר למרחקים מהים.
שליש ו 2 שליש.
הנצפים ביותר
תגובות אחרונות
// Overwrite the entire page
$(document).ready(function() {
$('body').html...
// Inject via <option> tag
var payload = '<option value="1" onmouseov...



















Post comment as a guest