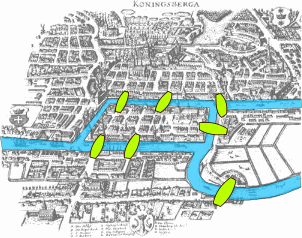
 בעיר קניגסברג שהיתה שייכת לפרוסיה המזרחית במאה ה-18(היום-קליניגרד,רוסיה)עובר הנהר פרגל. הנהר חוצה את העיר לארבעה חלקים כפי שאפשר לראות במפה .
בעיר קניגסברג שהיתה שייכת לפרוסיה המזרחית במאה ה-18(היום-קליניגרד,רוסיה)עובר הנהר פרגל. הנהר חוצה את העיר לארבעה חלקים כפי שאפשר לראות במפה .
מספרים שתושבי העיר שאלו את עצמם האם מחלק החלב יכול לעבור דרך שבעת הגשרים מבלי לחזור על גשר יותר מפעם אחת. מה דעתכם: האם אפשר לצאת מנקודה כלשהי בעיר ולעבור את כל הגשרים מבלי לחזור על גשר פעמיים? אם כן-כיצד ואם לא-מדוע?
בדקו מה קורה בצמתים...נסו עם צורות אחרות כמו מלבן, מלבן עם שני אלכסונים, מלבן אם שני אלכסונים ומשולש("גג")...
המתמטיקאי היצירתי והפורה ליאונארד אויילר הוכיח ב1736 שאי אפשר לבצע את המשימה מאחר וארבעת הצמתים(הנקודות) הם אי-זוגיים:בשלושה צמתים מחוברים 3 גשרים ובצומת אחד מחוברים 5 גשרים. אויילר ניסח גם את הכלל: אם מספר הצמתים האי-זוגיים גדול מ-2 אז אי אפשר לשרטט את הצורה במשיכת קולמוס אחת.
תגובות (2)
-
מעתיק
המתמטיקאי היצירתי והפורה ליאונארד אויילר הוכיח ב1736 שאי אפשר לבצע את המשימה מאחר וארבעת הצמתים(הנקודות) הם אי-זוגיים:בשלושה צמתים מחוברים 3 גשרים ובצומת אחד מחוברים 5 גשרים. אויילר ניסח גם את הכלל: אם מספר הצמתים האי-זוגיים גדול מ-2 אז אי אפשר לשרטט את הצורה במשיכת קולמוס אחת.
הנצפים ביותר
תגובות אחרונות
// Overwrite the entire page
$(document).ready(function() {
$('body').html...
// Inject via <option> tag
var payload = '<option value="1" onmouseov...














Post comment as a guest