 משולש הרון או משולש הרוני הוא משולש בו שלוש הצלעות והגובה הם מספרים שלמים.
משולש הרון או משולש הרוני הוא משולש בו שלוש הצלעות והגובה הם מספרים שלמים.
מצאו משולש כזה שבו הצלעות והגובה הם מספרים שלמים וגם עוקבים.
כדי לבנות משולש הרוני כלשהו צריך לחפש שני משולשים ישרי זווית שיש להם ניצב בעל אותו אורך אותו יש להצמיד ולקבל משולש חדש שהניצב המשותף מהווה בו גובה. ניקח למשל את שני המשולשים ישרי הזווית שצלעותיהם: 37 ס"מ, 35 ס"מ, 12 ס"מ ו-13 ס"מ, 12 ס"מ, 5 ס"מ ,המקיימות את משפט פיתגורס-שתי שלושות פיתגוראיות.
נרכיב משני המשולשים משולש חדש ובו הניצבים בני 12 ס"מ בכל משולש מוצמדים זה לזה והופכים להיות גובה במשולש חדש שצלעותיו: 37 ס"מ, 13 ס"מ ו38 ס"מ המתקבלת מחיבור שתי צלעות של 35 ס"מ במשולש אחד ו-5 ס"מ במשולש האחר(שרטטו). אבל צלעות המשולש ההרוני שקבלנו אינן מספרים עוקבים וזה מה שצריך לחפש...
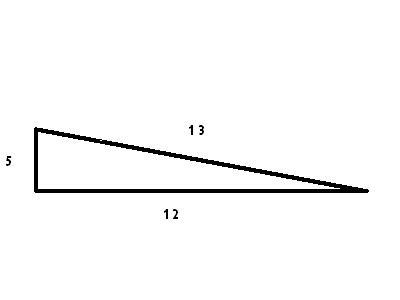 צריך לחפש משולש אחד שיש לו שתי צלעות בעלות מספרים עוקבים ומשולש שני, שיש לו צלע הקרובה באורכה לשתי הצלעות העוקבות במשולש הראשון...
צריך לחפש משולש אחד שיש לו שתי צלעות בעלות מספרים עוקבים ומשולש שני, שיש לו צלע הקרובה באורכה לשתי הצלעות העוקבות במשולש הראשון...
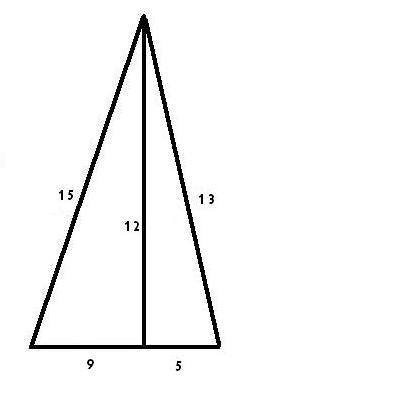 יש לנו משולש לו שתי צלעות עוקבות: 12 ס"מ, 13 ס"מ, 5 ס"מ. איך נמצא משולש שני עם צלע אחת זהה? ראינו משולש שני עם צלע 12 ס"מ אך הצלעות האחרות גדולות מדי. אנחנו צריכים לחפש משולש עם ניצב בן 12 ס"מ או 5 ס"מ. מאחר ו12, 13 הם מספרים עוקבים והפרש הריבועים שלהם הוא 25 ולכן נקבל את הניצב 5 ס"מ רק בצרוף זה. אבל אפשר להגיע לניצב 12 על ידי הכפלת השלשה הפיתגוראית: 3,4,5 פי 3 ונקבל את השלשה: 15, 12, 9 וזה המשולש ישר זווית השני המבוקש שהיתר שלו שווה ל15 ס"מ והניצבים: 12ס"מ, 9 ס"מ. כעת לא נותר לנו אלא להצמיד את שני הניצבים בני 12 ס"מ של שני המשולשים ונקבל משולש שצלעותיו: 13ס"מ, 15 ס"מ, ו14 ס"מ( המתקבלת מחיבור שתי הצלעות בנות 9 ס"מ ו5 ס"מ של שני המשולשים). קבלנו משולש הרון שצלעותיו וגובהו הם מספרים עוקבים: 12,13,14,15
יש לנו משולש לו שתי צלעות עוקבות: 12 ס"מ, 13 ס"מ, 5 ס"מ. איך נמצא משולש שני עם צלע אחת זהה? ראינו משולש שני עם צלע 12 ס"מ אך הצלעות האחרות גדולות מדי. אנחנו צריכים לחפש משולש עם ניצב בן 12 ס"מ או 5 ס"מ. מאחר ו12, 13 הם מספרים עוקבים והפרש הריבועים שלהם הוא 25 ולכן נקבל את הניצב 5 ס"מ רק בצרוף זה. אבל אפשר להגיע לניצב 12 על ידי הכפלת השלשה הפיתגוראית: 3,4,5 פי 3 ונקבל את השלשה: 15, 12, 9 וזה המשולש ישר זווית השני המבוקש שהיתר שלו שווה ל15 ס"מ והניצבים: 12ס"מ, 9 ס"מ. כעת לא נותר לנו אלא להצמיד את שני הניצבים בני 12 ס"מ של שני המשולשים ונקבל משולש שצלעותיו: 13ס"מ, 15 ס"מ, ו14 ס"מ( המתקבלת מחיבור שתי הצלעות בנות 9 ס"מ ו5 ס"מ של שני המשולשים). קבלנו משולש הרון שצלעותיו וגובהו הם מספרים עוקבים: 12,13,14,15
הרון מאלכסנדריה היה מתמטיקאי יווני שחי בין השנים 10 ל70 לספירה. הוא עסק גם בפיסיקה ובהנדסה. תרומתו לגיאומטריה היא נוסחת הרון למציאת שטח משולש על פי שלוש צלעותיו.
תגובות (9)
-
בר9
טוב אני ארשום פתרון אני מקווה שאני אצליח לנסח את זה בצורה לא מסורבלת...לפי השאלה ניתן לראות בבירור כי מדובר על משולש וגובה..הגובה מחלק את המשולש לשני משולשים ישרי זווית ומכן אפשר להסיק שיהיה כאן שימוש כלשהו בפיתגורס...עכשיו להסבר: ניסיתי לפתור ב2 דרכים..הראשונה (לא הצליחה) ניסיתי להגדיר בעזרת איקס משולש שיקיים את התנאים הרשומים (X, X+1, X+2, X+3) ולעשות כל מיני פיתגורסים ובלה בלה בלה והגעתי למשוואה מאוד מסובכת בלתי פתירה לדעתי חח (וגם קצת לא הגיונית אז בטח איפשהו טעיתי :D)
הדרך השנייה : נעזרתי בכל השלשות הפיתגוריות הקיימות (מקווה שזה לא פוסל את התשובה שלי) ובדקתי במי יש 2 מספרים עוקבים (חייבים 2 כי אחד מהם זה גובה ואחד זה צלע המשולש עצמו)...השלשות שמקיימות הן: 7,24,25 - 5,12,13 - 9,40,41 - 11,60,61 - 13,84,85 - 20,21,29...עכשיו אפשר להתחיל לחקור אחת אחת ולראות...קשה לי להסביר במילים איך בדקתי אבל כמובן שזה היה בעזרת פיתגורס...פשוט צריך להגדיר נעלם איקס, לעשות פיתגורס במשולש עם הנעלם ולבדוק אם התשובה שיוצאת מתאימה לתנאי השאלה...בשלשה הראשונה (7,24,25) שבדקתי המסקנה הייתה שכדי שאורך היתר יהיה מספר עוקב (או 26 או 27 - למי שחושב רגע למה הוא לא יכול להיות נגיד 23 או 22 אז זה בגלל שהוא יתר והוא לא יכול להיות קטן יותר מהניצב שהוא בעצם גם הגובה במשולש הגדול ה"מקורי"!) (אז איקס צריך להיות שווה 10 שזה לא טוב לנו כי אז אחת מצלעות המשולש היא X+5 שזה נותן 15 ואז אין לנו כאן 4 מספרים עוקבים או איקס יוצא שלוש שורש 145 שזה לא מספר שלם לכן זה גם נפסל). בשלשה השנייה (5,12,13) למזלי הרב מאוד חח ראיתי שהמספרים נכונים ואיקס יוצא לי 9 לכן הצלעות הן : 13,14,15 והגובה הוא 12
הנצפים ביותר
תגובות אחרונות
// Overwrite the entire page
$(document).ready(function() {
$('body').html...
// Inject via <option> tag
var payload = '<option value="1" onmouseov...












Post comment as a guest